티스토리 뷰

1. 배열 (Array)
'배열'이란 같은 데이터형의 요소들이 동일한 크기로 순서를 갖고 나열되어 있는 집합이다. 같은 이름을 사용하지만 첨자에 의해 서로 구분되는 집단적인 데이터 저장 영역을 의미한다. 따라서 데이터마다 변수 이름을 따로 두지 않으므로 처리가 훨씬 수월하다는 장점이 있다.

C언어의 경우 크기가 n인 배열 arr의 첫 번째 요소는 arr[0], 두 번째 요소는 arr[1], ··· 마지막 n번째 요소는 arr[n-1]로 나타낸다. arr[0], arr[1], arr[2], ···, arr[n-1]처럼 각각의 요소는 arr[i]로 표현되는데, 이때 i를 '첨자'라고 하며, arr과 같은 집단의 묶음을 '배열이름'이라고 한다. 배열은 첨자의 수에 따라 구분되는데, 첨자를 1개 사용하면 1차원 배열, 2개 사용하면 2차원 배열, 3개 사용하면 3차원 배열이라 한다.
2. 연결리스트 (Linked List)
배열 방식에서 삽입, 삭제 시 소요되는 연산 시간과 필요한 저장공간에 대한 한계를 개선한 자료구조이다. 연결리스트에서는 데이터가 저장될 때 다음 데이터의 위치 정보가 같이 저장된다. 삽입 데이터가 연속적으로 할당되는 방식이 아니기 때문에 연결하기 위해선 다음 데이터의 위치 정보도 함께 저장되어야 한다. 연결리스트는 데이터를 연결하는 방식에 따라 단순 연결리스트, 원형 연결리스트, 이중 연결리스트로 구분된다.
2-1. 단순 연결리스트 (Singly Linked List)
단순 연결리스트는 꼬리에 꼬리를 무는 방식으로 데이터가 저장될 때 다음 데이터의 위치 정보가 같이 저장된다. Head 포인터가 첫 번째 데이터의 위치 정보와 연결되어 있고, 마지막 데이터의 포인터는 NULL을 가리킨다.
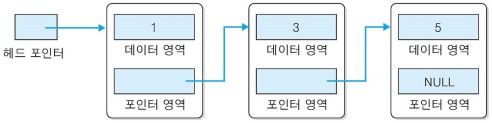
2-2. 원형 연결리스트 (Circular Linked List)
원형 연결리스트는 단순 연결리스트에서 마지막 노드가 첫 번째 노드를 가리키고 있어 원형 구조를 이루는 리스트다. 현재 노드의 이전 노드를 검색하려면 전체 리스트를 한 바퀴 순회해야 하는 단점이 있다. 이 문제를 해결해 연결리스트를 양방향으로 순회할 수 있는 리스트가 이중 연결리스트다.

2-3. 이중 연결리스트 (Doubly Linked List)
이중 연결리스트는 앞 노드와 뒤 노드의 위치를 저장할 링크 필드와, 데이터 필드로 구성되어 있어 양방향 순회가 가능하다.

※ 연결리스트를 배열과 비교했을 때
| 장점 | 1) 데이터의 앞, 뒤 노드의 참조 관계만 수정하면 삽입, 삭제가 가능 2) 연산 시 데이터의 위치나 전체 데이터 수와 관계없이 일정한 성능으로 동작 3) 노드는 독립적인 공간의 메모리이기 때문에 개수의 제한이 없으며 재사용 또한 가능 |
| 단점 | 1) 구현이 복잡하고 검색 성능이 떨어짐 2) 특정 인덱스의 데이터를 검색하더라도 순차적으로 검색해야 하므로 데이터 접근 시간이 소요됨 |
3. 스택 (Stack)
스택은 데이터의 삽입과 삭제가 한쪽 방향에서만 일어나는 구조다. 다음과 같은 동전 케이스는 동전을 넣는 곳과 빼는 곳의 방향이 같아 가장 최근에 들어간 동전이 가장 먼저 나오는 스택의 예이다. 이와 같은 스택은 가장 나중에 삽입된 데이터가 가장 먼저 삭제되므로 후입 선출(LIFO : Last-In First-Out) 구조라고도 한다.

4. 큐 (Queue)
큐는 한쪽 방향으로 데이터가 삽입되고 반대 방향으로 데이터가 삭제되는 구조다. 다음과 같은 마트 계산대에서는 계산대에 먼저 도착한 고객이 먼저 계산하고 나가는데, 이는 큐의 예시이다. 이와 같은 큐는 가장 먼저 삽입된 데이터가 가장 먼저 삭제되므로 선입 선출(FIFO : First-In First-Out) 구조라고도 한다.

5. 덱 (Deque, Double-Ended Queue)
덱은 양쪽 끝에서 삽입과 삭제가 모두 가능한 형태이다. 두 개의 포인터를 사용하여 양쪽에서 삽입과 삭제를 발생시킬 수 있다. 스택과 큐를 합친 형태로 생각할 수 있다.
스크롤 - 입력이 한쪽 끝으로만 가능하도록 설정한 데크 (입력 제한 데크)
셸프 - 출력이 한쪽 끝으로만 가능하도록 설정한 데크 (출력 제한 데크)

6. 트리 (Tree)
트리는 나무를 뒤집은 모습으로 계층 구조를 표현하기에 적합하다.

위 사진에서 원을 '노드(node)'라 하고, 노드와 노드를 연결하는 선을 '간선(link, line, edge)'라 한다. 특히 가장 위에 위치한 노드를 '루트 노드(root node)'라 하는데, 이는 한 개만 있어야 한다. 그리고 윤리교육과, 국어교육과 노드와 같이 마지막에 위치한 노드를 '단말 노드(terminal node)' 또는 '리프 노드(leaf node)'라 한다.

트리에서 임의의 노드를 선택하면 이 노드와 이 노드 아래에 있는 노드들은 다시 트리 구조가 된다. 이런 구조를 '서브 트리(subtree)'라 한다. 임의의 노드의 조상과 자손을 지칭할 수 있는데, 임의의 노드 바로 위에 있는 노드를 '부모 노드(parent node)'라 하고, 바로 아래에 있는 노드를 '자식 노드(children node)'라 한다. 그리고 같은 부모 노드를 가지는 노드들을 '형제 노드(sibling node)'라 한다. 루트 노드에서 임의의 노드까지 방문한 노드의 수를 '레벨(level)'이라 하는데, 노드 E의 레벨은 3이 된다. 그리고 트리의 최대 레벨을 '깊이(depth)'라 하는데, [그림 10] 트리의 최대 레벨은 4이므로 깊이는 4이다.
6-1. 일반 트리
상술한 구조를 갖는 것을 일반 트리라고 한다.
6-2. 이진 트리 (Binary Tree)
각각의 노드가 최대 2개의 자식 노드를 가지는 트리 자료 구조로, 자식 노드를 각각 왼쪽 자식 노드와 오른쪽 자식 노드라고 한다.
※ 트리의 성질 (1~5는 일반 트리, 6,7까지 만족하면 이진 트리)
(1) 임의의 노드에서 다른 노드로 가는 경로(path)는 유일하다.
(2) 회로(cycle)가 존재하지 않는다.
(3) 모든 노드는 서로 연결되어 있다.
(4) 간선을 하나 자르면 트리가 2개로 분리된다.
(5) 간선의 수는 노드의 수에서 1을 뺀 것과 같다.
(6) 루트노드를 중심으로 2개의 트리로 갈라진다.
(7) 나뉘어진 두 서브노드들 역시 이진트리여야 한다.
7. 그래프 (Graph)
그래프는 연결되어 있는 객체 간의 관계를 표현할 수 있는 자료구조이며, 수학자 레온하르트 오일러(Leonhard Euler)에 의해 처음 창안되었다. 그래프는 정점(vertex)과 정점들을 연결하는 간선(edge)으로 구성된다. 일반적으로 정점은 원으로 표현하고 간선은 화살표나 선분으로 표현한다. 변을 화살표로 나타내는 경우에는 해당 방향으로만 이동할 수 있으며, 이러한 그래프를 유향 그래프(Directed Graph)라고 한다. 간선은 특정한 수치를 가질 수 있는데, 이를 가중치(Weighted Value)라고 한다. 그래프는 도시와 도로로 비유될 수도 있기 때문에 두 지점 간의 최단 경로를 구하는 데 널리 이용된다.
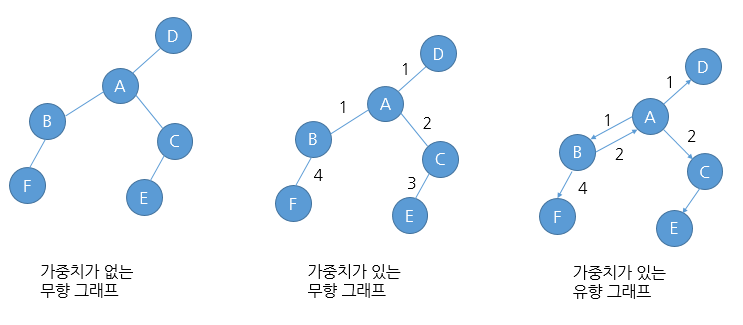
※ 트리와 그래프의 차이
| 트리 | 그래프 | |
| 정의 | 그래프의 한 종류 DAG(Directed Acyclic Graph, 방향성이 있는 비순환 그래프)의 한 종류 |
노드(node)와 그 노드를 연결하는 간선(edge)을 하나로 모아 놓은 자료구조 |
| 방향성 | 방향 그래프(Directed Graph) | 방향 그래프(Directed) 무방향 그래프(Undirected) 모두 존재 |
| 사이클 | 사이클(Cycle) 불가능. 비순환 그래프(Acyclic Graph) | 사이클(Cycle) 가능. 자체 간선(self-loop)도 가능. 순환 그래프(Cyclic), 비순환 그래프(Acyclic) 모두 존재 |
| 루트 노드 | 한 개의 루트 노드만이 존재. 모든 자식 노드는 한 개의 부모 노드만을 가짐 |
루트 노드의 개념이 없음 |
| 부모-자식 | 부모-자식관계 top-bottom 또는 bottom-top으로 이루어짐 |
부모-자식의 개념이 없음 |
| 모델 | 계층 모델 | 네트워크 모델 |
| 순회 | DFS, BFS안의 Pre-, In-, Post-order | DFS, BFS |
| 간선의 수 | 노드가 N인 트리는 항상 N-1의 간선을 가짐 | 그래프에 따라 간선의 수가 다름. 간선이 없을 수도 있음 |
| 경로 | 임의의 두 노드 간의 경로는 유일 | - |
| 예시 및 종류 | 이진 트리, 이진 탐색 트리, 균형 트리(AVL 트리, red-black 트리), 이진 힙(최대힙, 최소힙) 등 | 지도, 지하철 노선도의 최단 경로, 전기 회로의 소자들, 도로(교차점과 일방 통행길), 선수 과목 |
- Total
- Today
- Yesterday
- Browser Object Model
- keyword
- Navigator 객체
- 키워드
- 컴파일
- 리액트 #React #props #state #javascript
- window 객체
- stdio.h
- 변수
- Document Object Model
- location 객체
- Char
- 자료형
- DOM
- Screen 객체
- bom
- c언어
- gcc
- History 객체
- short
- long
- int
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
